A-Stern

Der $A^\star$-Algorithmus[1] (im folgenden $A^\star$ genannt) wird verwendet, um in einem Baum oder allgemein in einem Graphen den kürzesten Pfad zwischen zwei Knoten zu finden. Um $A^\star$ anwenden zu können, müssen die Kanten mit Kosten versehen sein. Gesucht ist nun der kürzeste (bzw. billigste) Pfad zwischen zwei Knoten.

Bei der Breitensuche wird keine «intelligente» Auswahl der Knoten in der Open-List getroffen, die Knoten werden in willkürlicher Reihenfolge verarbeitet. Der $A^\star$ ist eine Verfeinerung dieser Verfahren, wobei folgendermassen immer der vielversprechendste Knoten weiterverarbeitet wird. Es wird abgeschätzt, wie «gut» ein Knoten ist, indem eine Bewertungsfunktion berechnet wird. Die Kosten eines Knotens $N$ beinhalten zwei Beiträge: einerseits die Kosten vom Startknoten bis zu $N$ (wie bei Dijkstra) und andererseits die geschätzten Kosten von $N$ bis zum Zielknoten. Diese Bewertungsfunktion $f(N)$ für einen Knoten $N$ wird also folgendermassen definiert:

A-Stern

$$f(N) = g(N) + h(N)$$

wobei $g(N)$ die Kosten des Pfades vom Startknoten zu $N$ darstellt und $h(N)$ die geschätzten Kosten eines optimalen Pfades von $N$ zum Zielknoten darstellt.

Bei der Schätzung muss gelten:

$$h(N) \geq h^*(N)$$

wobei $h^\star(N)$ die tiefstmöglichen Kosten für die Verbindung von $N$ zum Zielknoten sind (dieser Pfad muss nicht zwingen über den vorhanden Graphen verlaufen. A* könnte andernfalls falsche Resultate liefern, wenn plötzlich eine neue, direktere Verbindung von N zum Ziel gebaut wird. Deshalb ist die Luftlinie eine gute heuristik - schneller geht es mit herkömmlichen Gesetzen der Physik nicht).

Die Funktion $h$ ist eine sog. Heuristik, also eine Abschätzung des wahren Werts. So kann die Suche nach dem optimalen Pfad oft wesentlich beschleunigt werden, was beim $A^\star$ ausgenutzt wird. Man kann zeigen, dass der immer den kürzesten Weg findet, wenn es einen gibt.

Beispiel

Gesucht ist der schnellste Weg von Würzburg nach Saarbrücken. Durch Abstraktion der Karte wurde der folgende gewichtete Graphen erzeugt. Zusätzlich kennt man für jeden Knoten eine Heuristik, nämlich die Distanz der Luftlinie nach Würzburg:

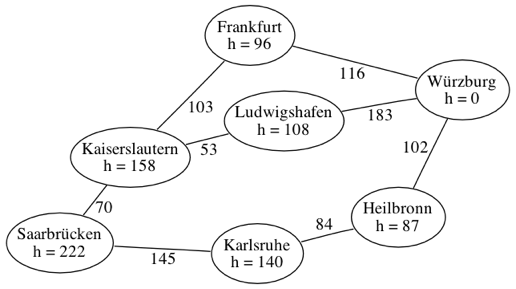
Schritt 1

Saarbrücken

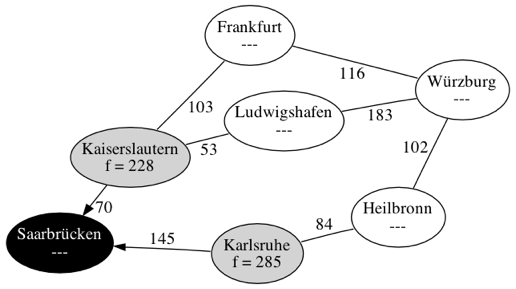
Start beim Ziel. Für alle anliegenden Knoten $f(Knoten) = g(Knoten) + h(Knoten)$ berechnet, also "Distanz vom Ziel bis zum Knoten" + "Luftlinie vom Knoten bis zum Start".

Kaiserlautern

$f = 70 + 158 = 228$

Karlsruhe

$f = 145 + 140 = 285$

• Orientiere die Kanten in Richtung des Verbindungspfades

• Markiere Saarbrucken als besucht

• Besuche den Knoten mit dem kleinsten $f$-Wert: Kaiserslautern

Schritt 2

Kaiserlautern

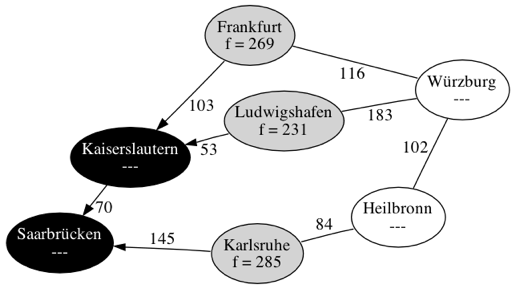
Frankfurt

$f = 70 + 103 + 96 = 269$

Ludwigshafen

$f = 70 + 53 + 108 = 231$

• Orientiere die Kanten in Richtung des Verbindungsknotens

• Markiere Kaiserslauten als besucht

• Besuche den Knoten mit dem kleinsten $f$-Wert: Ludwigshafen

Schritt 3

Ludwigshafen

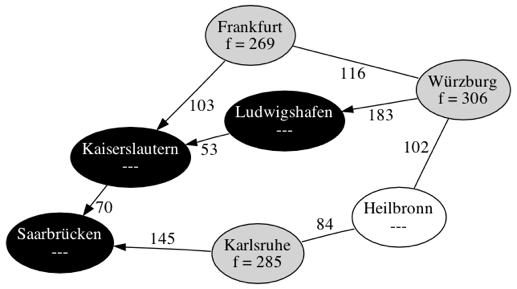
Würzberg

$f = 70 + 53 + 183 + 0 = 306$

• Orientiere die Kanten in Richtung des Verbindungsknotens

• Markiere Kaiserslauten als besucht

• Besuche den Knoten mit dem kleinsten $f$-Wert: Frankfurt

Schritt 4

Frankfurt

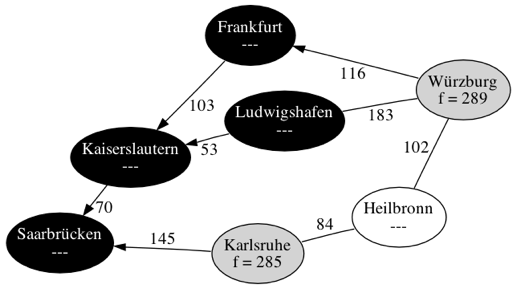
Würzbeburg

$f = 70 + 103 + 116 + 0 = 289$

• Da $f=289$ kleiner als $f=306$ ist, wird der Pfad über Frankfurt gewählt.

• Orientiere die Kanten in Richtung des Verbindungsknotens

• Markiere Frankfurt als besucht

• Besuche den Knoten mit dem kleinsten $f$-Wert: Karlsruhe

Schritt 5

Karlsruhe

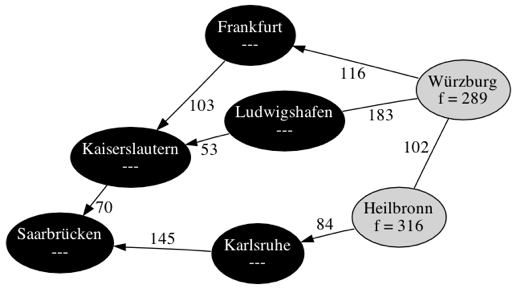
Heilbronn

$f = 145 + 84 + 87 = 316$

• Orientiere die Kanten in Richtung des Verbindungsknotens

• Markiere Karlsruhe als besucht

• Besuche den Knoten mit dem kleinsten $f$-Wert: Würzburg

Schritt 6

Würzburg

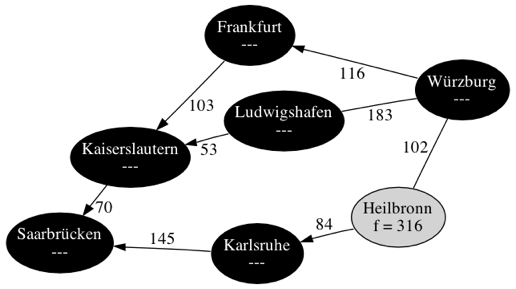
• Fertig 🥳

• Der kürzeste Weg von Würzburg nach Saarbrücken ist über Frankfurt und Kaiserslauten gefunden.

Aufgabe 1: Vergleich Dijkstra und A*-Algorithmus

Berechnen Sie für das Folgende Strassennetz den kürzesten Weg von nach München nach Frankfurt mit dem A*-Algorithmus. Die Entfernungen zwischen den Städten sind in der Abbildung angegeben.

Als Heuristik sollen folgende Luftlinien-Entfernungen verwendet werden:

Augsburg <--> München: 43 km
Erfurt <--> München: 342 km
Frankfurt <--> München: 353 km
Karlsruhe <--> München: 260 km
Kassel <--> München: 446 km
Mannheim <--> München: 311 km
München <--> München: 0 km
Nürnberg <--> München: 151 km
Würzburg <--> München: 229 km

SSR

Vergleich der Algorithmen

Die drei Algorithmen Breitensuche, Dijkstra und A-Stern-Algorithmus unterscheiden sich in ihrer Vorgehensweise und in ihrer Effizienz. Die folgende Tabelle gibt einen Überblick:

Aufgabe 2

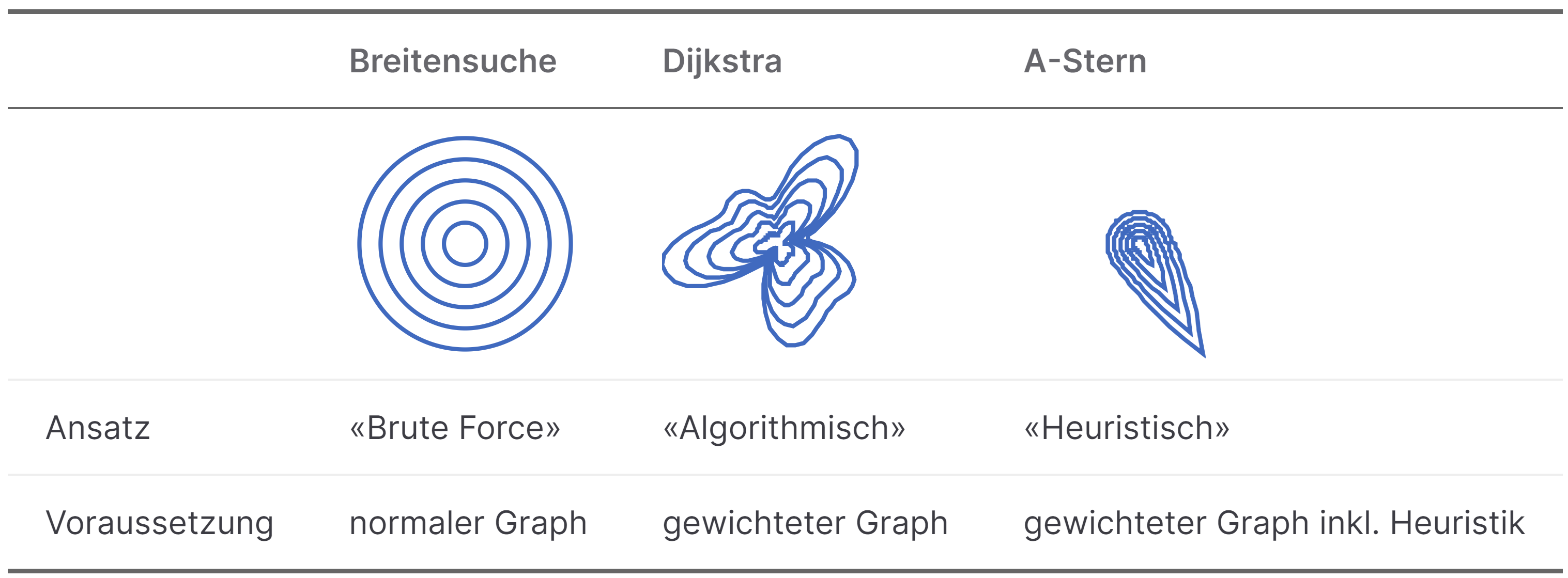
Auf der verlinkten Seite können Breitensuche, Dijkstra und A-Stern miteinander vergleichen werden. Testen Sie die Seite aus und beantworten Sie folgende Fragen:

• Was ist «Breadth First»?

• Was ist «Depth First»?

• Wofür stehen die Farben wenn man bei Terrain den Eintrag Simplex Terrain wählt. Welchen Einfluss haben diese auf den A-Stern-Algorithmus?

👉 pathfindout.com

⭐ Zusatzaufgabe 3

Der A-Stern-Algorithmus kommt auch in Computer-Spielen zu Einsatz: Lesen Sie den folgenden Beitrag durch und testen Sie die tollen (und teilweise interaktiven) Visualisierungen:

👉 redblobgames.com