P-NP

Algorithmen mit einer polynomialen Laufzeit von $n^2$ oder allgemein $n^k$ skalieren bereits schlecht. Das bedeutet, dass sie bei einem grösseren Input kaum brauchbar sind weil sie das Resultat nicht mehr in nützlicher Zeit liefern können. Sie gelten aber immer noch als effizient. Man muss die Input-Länge kontrollieren.

Algorithmen mit exponentieller Laufzeit, also $2^n$ oder $k^n$, werden nicht mehr als effizient bezeichnet. Ihre Komplexität wächst so stark mit steigendem Input, dass sehr bald schon keine Resultate mit vernünftigem Aufwand möglich sind.

Vergleich Komplexität@

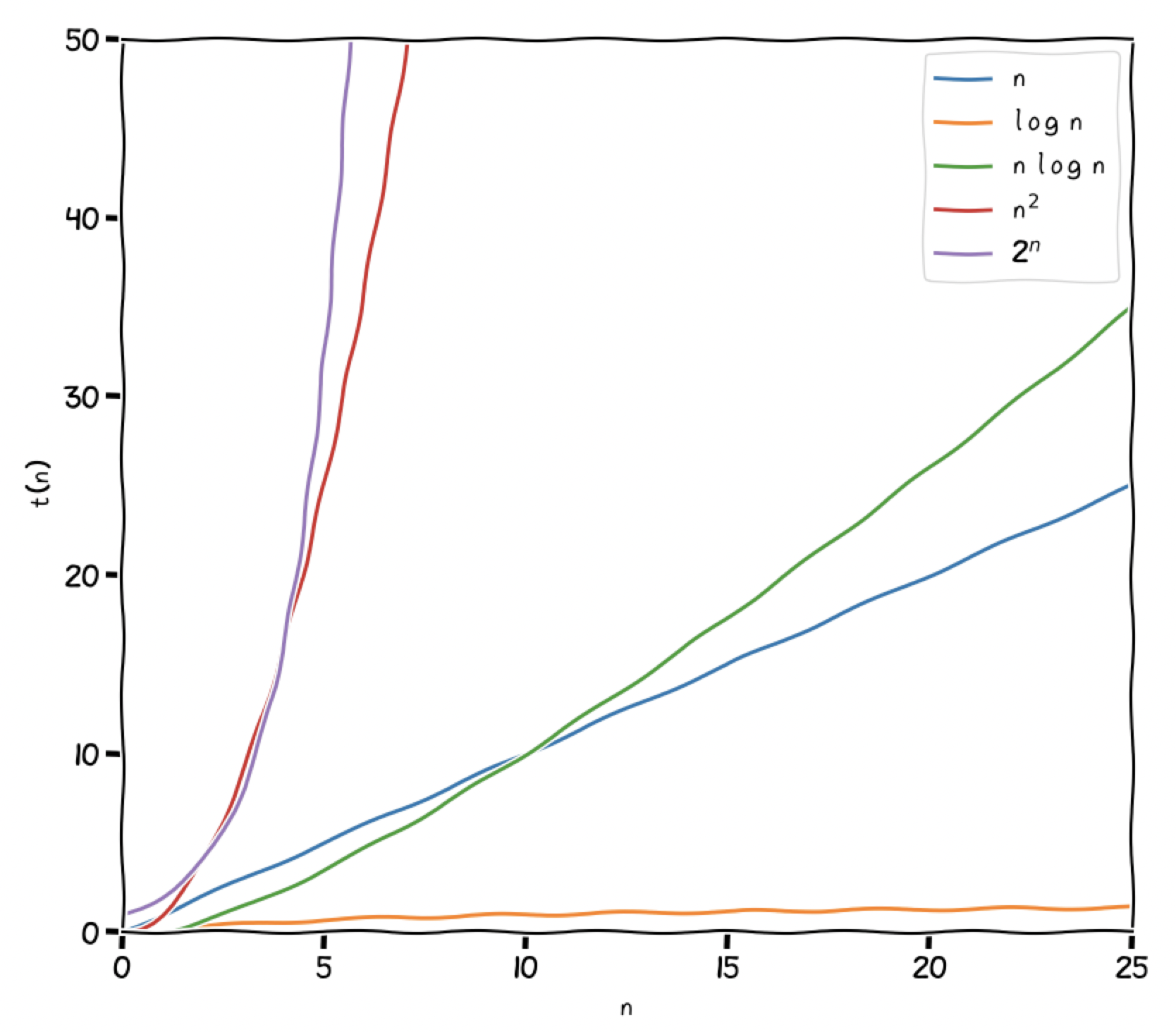
Für viele Probleme der Informatik hat man noch keine effiziente Algorithmen gefunden, also solche mit polynomialer Laufzeit oder besser.

Komplexitätsklasse P

Die Komplexitätsklasse $P$ enthält die Probleme, für die eine deterministische Turingmaschine (etwa ein konventioneller Computer) existiert, die das Problem in polynomialer Laufzeit löst.

Komplexitätsklasse NP

Die Komplexitätsklasse $NP$ enthält die Probleme, von denen sich in polynomialer Laufzeit mit einer deterministischen Turingmaschine entscheiden lässt, ob eine vorgeschlagene Lösung zutrifft.

P-NP-Problem

Unbekannt ist, ob die beiden Klassen $P$ und $NP$ identisch sind, ob also auch die schwersten Probleme der Klasse $NP$ deterministischen Maschinen effizient lösbar sind.

P-NP-Problem@

Beispiele

Faktorisierung

Ein solches Beispiel ist die Faktorisierung einer Zahl in ihre Primfaktoren.

$$\text{z.B.} 91 = 7 \cdot 13 \qquad \text{oder} \qquad 12 = 2 \cdot 2 \cdot 3$$

Diese Aufgabe scheint einfach, wird aber für sehr grosse Zahlen sehr aufwändig!

Es ist kein polynomiales Faktorisierungsverfahren bekannt – es kann aber auch nicht ausgeschlossen werden, dass es ein solches gibt! Dieses sogenannte P-NP-Problem ist eines der grossen ungelösten Probleme der theoretischen Informatik.

SAT – Erfüllbarkeitsproblem der Aussagenlogik

Das Erfüllbarkeitsproblem der Aussagenlogik (SAT, von englisch satisfiability) ist ein Entscheidungsproblem der theoretischen Informatik. Es beschäftigt sich mit der Frage, ob eine gegebene aussagenlogische Formel $F$ erfüllbar ist. Mit anderen Worten: Existiert eine Belegung der Variablen von $F$ mit den Werten wahr oder falsch, so dass $F$ zu wahr ausgewertet wird?

Beispiel einer solchen aussagelogsichen Formel:

$$F = (A \vee C) \wedge (\neg A \vee D \vee \neg E) \wedge (B \vee \neg D \vee E)$$

Notation wie wir es von Python kennen:

F = (A or C) and (not A or D or not E) and (B or not D or E)

Aufgabe

Finden Sie eine Belegung der boolean Variablen A - E, womit F True ergibt.

SAT gehört zur Komplexitätsklasse NP. Jedes Problem aus NP kann in polynomieller Zeit auf SAT zurückgeführt werden (Polynomialzeitreduktion).

Eine deterministische Turingmaschine (im allgemeinen also ein sequenziell abgearbeitetes Programm, das endet) kann SAT in exponentieller Zeit entscheiden, zum Beispiel durch das Aufstellen einer Wahrheitstabelle. Es ist kein effizienter Algorithmus für SAT bekannt und es wird allgemein vermutet, dass ein solcher Polynomialzeitalgorithmus nicht existiert. Die Frage, ob SAT in polynomieller Zeit gelöst werden kann, ist äquivalent zum P-NP-Problem.

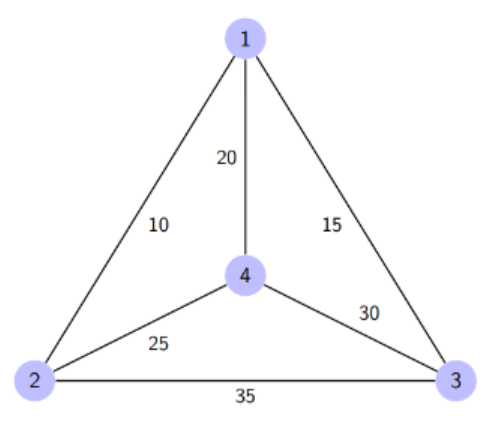
TSP - Travelling Salesman Problem

Das Travelling Salesman Problem (TSP) ist ein klassisches Problem der Kombinatorik und der theoretischen Informatik. Es handelt sich um die Frage, wie der kürzeste Rundweg durch eine Menge von Städten gefunden werden kann, wenn die Entfernungen zwischen den Städten bekannt sind. Das Problem ist NP-vollständig und es ist bis Dato kein effizienter Algorithmus bekannt, der das Problem in polynomieller Zeit löst.

TSP

Finden Sie den kürzesten Rundweg durch die folgenden Städte:

SSR